CS231n 강의를 듣고 내용을 공부하면 정리하였습니다.
Lecture 2 | Image Classification - YouTube
일부 이미지는 본 강의 자료에서 발췌하여 사용하였습니다.
Image Classification
다음 dog의 이미지가 있다고 봅시다.

이 이미지를 보고 dog인지, 혹은 cat인지 판단하고 구별하는 것이 Image Classification입니다.
Image Classification의 목표는 이미지를 Input으로 받아 Output으로 Lable을 리턴하는 것입니다.
이미지 데이터의 구조는 숫자로 구성된 3D 배열 형태입니다.

3차원 데이터로, Column, Row, Color Channel (컬러 채널, Gray는 1, RGB는 3) 로 구성되어있습니다.
이미지 데이터를 다루면서 아래와 같은 경우 데이터를 다루기 힘들어집니다.
| Viewpoint Variation | 시점 변화. 이미지를 보는 방향이나 위치가 달라질 경우 |
| Illumination | 밝기가 달라질 경우 |
| Deformation | 객체의 모습이 변형될 경우 |
| Occlusion | 객체의 모습이 일부 가려질 경우 |
| Background Clutter | 객체와 배경의 구분이 모호한 경우 |
| Intraclass Variation | 여러 객체가 있을 경우 |
과거의 Classification을 하드코딩을 통해 해결 하려던 사례가 있습니다.
이미지의 특징 Edge, Shape등을 찾아 어떻게 arrange되었는지 탐색하는 방법을 사용하였는데 당연히 많은 한계가 존재합니다.
그래서 Data-driven 방식으로 접근을 합니다.
- 이미지와 레이블로 구성된 데이터셋을 수집
- 머신러닝을 이용하여 Image Classifier를 학습
- test 이미지 셋에 대해 Classifier를 평가
이 방법은 Training(학습)통해 모델을 만들고,
Predict(예측)통해 Test 이미지에 대한 Label을 반환하는 것이 목적입니다.
어떤 방법들이 있는지 알아봅시다.
Nearest Neighbor Classifier (NN)
Nearest Neighbor Classifier(NN)은 지금은 사용하지 않는 방식입니다.
이 방법은 이름 그대로 근접한 이웃, 근접한 데이터들과의 관계로 분류를 합니다.
이 알고리즘이 예측하는 방법은 다음과 같습니다.

모든 학습용 이미지와 레이블들을 메모리 상에 올려 기억하게 한 후, 예측 단계에서는 모든 Training 이미지와 test이미지를 비교하여 제일 비슷한 이미지 레이블로 예측하는 것입니다.
그렇다면 NN이 데이터를 비교하는지 알아봅시다. NN은 Distance(거리)로 데이터를 비교합니다.
Training 이미지와 Test 이미지의 Pixel-wise 즉, 각 원소의 차의 절댓값을 구합니다.
계산을 위해 L1 distance (Manhattan distance) 멘하튼 거리라는 수식을 이용합니다.
(L1 distance 만 아니라 L2 distance도 있는데, 이 둘중 무엇을 사용할 것인지는 Hyperpaprameter로서 작용하게 됩니다.)
$$ d_{1}(I_{1},I{2})= \sum_{p}^{}\left | I_{1}^{p}-I_{2}^{p} \right | $$
위 식은 값을 비교한 후 차의 절댓값을 구하는 수식입니다.
모든 픽셀들의 값을 비교하여 Pixel-wise를 구한 후, 값들을 더합니다.
결과로 나온 값의 크기가 제일 작은 값(레이블 값이랑 유사할수록 비슷한 이미지)이 정답이 됩니다.
하지만 NN에는 여러 단점들이 존재합니다.
- 모든 데이터를 메모리에 올리기 때문에 메모리 사용량이 크다
- Training 데이터가 증가하면 Test 데이터의 결과까지의 시간은 선형적으로 증가한다.
다음은 K-NN에 대해 알아봅시다.
K-Nearest Neighbor (K-NN)

K-Nearest Neighbor (KNN)은 k개의 가장 가까운 이미지들을 찾고 k개의 이미지들이 다수결로 boarding하는 방식입니다.
위 이미지를 보면 2번째 NN과 비교하여 3번째 K-NN(k=5)일 때 더 정갈한 모습을 보입니다.
K-NN은 NN보다 성능이 좋습니다.

이미지는 k값에 따른 분류 모습입니다.
NN과의 비교를 위해 여기서 하나 가정을 해봅시다.
Training 데이터에 있는 이미지를 NN으로 분류하면 정확도는 100% 입니다.
왜냐하면 Test한 Training 데이터와 동일한 이미지가 트레이닝 셋에 존재하기 때문입니다.
이제 K-NN에 트레이닝 셋에 적용한다면 결과는 상황에 따라 달라지게 됩니다.
K-NN 알고리즘의 클래스의 우선순위에 따라 같은 Training 데이터여도 예측 값이 달라지기 때문입니다.
위에서 말했듯이 어떤 L1, L2 distance를 사용할 것인지 결정하는것은 Hyperparameter로서 작용한다 하였습니다.
그리고 어떤 k값 또한 Hyperparamter로 작용합니다.
Hyperparameter는 문제, 주어진 환경에 따라 퍼포먼스가 제일 잘 나오는 것을 선택해야 좋은 결과를 얻겠죠.
그러면 어떻게 Hyperparameter를 튜닝해야할지 알아봅시다.
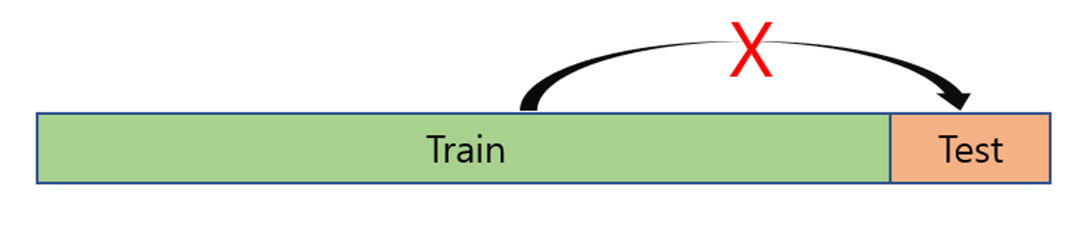
먼저 주의해야 할점은 Hyperparameter를 바꿔가면서 test 데이터에 적용하는 것은 매우 안 좋은 방법입니다.
Test 데이터는 성능 평가를 위해 남겨둬야 하는 데이터이므로 함부로 사용하면 안됩니다.

그래서 Training 데이터의 약 20% 정도를 validation 데이터로 만들어 Hyperparameter를 튜닝하기위한 공간으로 만듭니다.

만약 Training data가 적으면 Cross-validation 활용합니다.
Cross-validation은 fold 1,2,3,4를 학습한 후, 5에 validation → 2,3,4,5에서 학습하고 5에서 validation… 식으로 반복합니다.
이 방법을 통해 Hyperparameter를 튜닝 할 수 있습니다.
다음은 k값에 따른 5-fold Cross_validation의 Accuracy를 나타낸 그래프입니다.

각 K에 대해 5개씩 점이 찍혀있습니다. 점은 각각의 output을 나타냅니다.
파란색 실선이 평균값이며, 평균값이 제일 높은것은 k=7 정도일 때입니다.
따라서 k가 7에 가까울 때 가장 높은 정확도를 나타냅니다.
K-NN은 현실에서 사용하기 힘든 알고리즘입니다.
실제로는 K-NN은 현실에서는 아래와 같은 이유로 사용하지 않습니다.
- 테스트 타임에 성능이 매우 안좋다
- distance matrix는 정확한 예측이 어렵다.
- Curse of Dimension (차원이 증가할수록 문제가 지수적으로 증가)
아래 4개의 이미지를 봅시다.

Tinted, shifted, messed up을 한 이미지와 original 이미지 모두 오리지널과 동일한 L2 distance값을 가집니다. 즉 같은 이미지라 인식하는 것이죠
Linear Classification
Linear Classification는 앞에 설명한 단점들을 해결하기 위한 방법입니다.
바로 Neural Network를 이용하는 것입니다.
Linear Classification은 Parameter 기반의 접근법을 이용합니다.
앞서 배운 Nearesst Neigbor는 Non-Parameter 입니다.
이제 Linear Classification의 수식을 알아봅시다.
$$ f(x,W) $$
다음 식에서 x값은 이미지, W는 paramter를 말합니다.
우리는 파라미터를 컨트롤 하여 이미지를 Classification 할 수 있습니다.
예시 이미지로 설명하겠습니다.

다음 32x32x3 크기의 이미지가 있다 생각합시다.
32x32x3 = 3072개의 이미지에 대한 데이터가 나옵니다.
이제 3072개의 픽셀 값을 한 개의 colum vector로 표현합니다.
결과적으로 이미지는 3072x1 벡터가 될 것입니다.
이제 수식을 통해 나타내봅시다.
10개의 Class가 있다고 가정해보겠습니다.
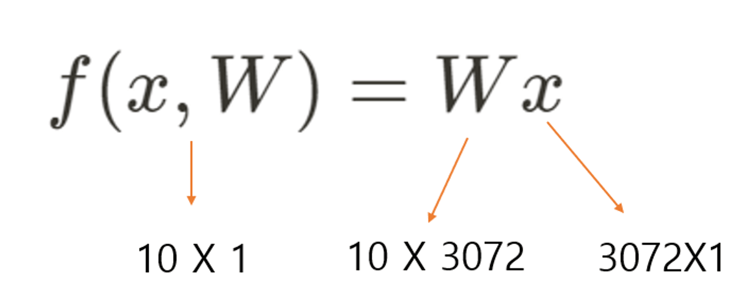
((f(x,W))는 10개의 Class를 나타내는 10x1 행렬입니다.
x값은 이미지로 32 X 32 X 3 이미지의 Column vector입니다.
위 식을 풀기 위해서 W는 10 X 3072 크기의 행렬이 되겠죠.
결과적으로 W = 10 X 3072 = 30720개의 파라미터를 갖게 됩니다.
물론 여기에 Bias값도 있습니다 (10X1)
이제는 30720+10개의 파라미터를 컨트롤해야 합니다.
이제 어떻게 예측을 하는지 알아봅시다.
4x1의 크기의 예시 이미지 colum vector가 있다고 합시다.

이 예제에서는 W = 3X4 , bias=3개로 15개의 파라미터를 가집니다.
예제의 결과의 Scroe는 Dog가 제일 높은 것을 볼 수 있는데, 이는 아직 학습이 이루어지지 않아 제대로 된 예측을 하지 못하기 때문입니다.
위 내용들을 정리하면 Linear Classifier는 이미지 내의 모든 픽셀값들에 대해 가중치를 곱하여 처리한 것의 합이라 할 수 있습니다.
하지만 이 방법의 단점 역시 존재합니다.
아래 이미지는 Cifar-10 데이터의 학습한 가중치를 시각적으로 표현한 모습입니다.

각 가중치들의 색상이 보이는데 이는 색상에 많이 의존한다는 의미입니다.
즉 Feature의 모습이 좋지 않아도 색상이 비슷하면 같은 Class로 인식해버리는 오류가 발생합니다.
또한 같은 Class의 이미지여도 정 반대의 색상이라면 다른 Class라 인식해버리기도 합니다.
Linear Classifier를 공간적으로 해석하면 다음과 같습니다.

이번 강의를 통해 Image Classification에 대해 배울 수 있었습니다.
NN, K-NN의 알고리즘에 대한 내용과 Linear Classification에 대해 더 자세히 알 수 있어 좋았습니다. 이번 글이 비슷한 공부하시는 분들께 도움이 되었으면 좋겠습니다.
'AI > CS231n' 카테고리의 다른 글
| [CS231n] Loss Function and Optimization 정리 (0) | 2024.08.29 |
|---|